Variance Ratio Test and Filter Rule
在 Do stock prices follow random walk over day and night? –– evidence from Chinese stock market 这篇论文中，我们使用了修改版的Variance Ratio Test和Filter Strategy分别在统计上和经济上检验了日内时段和隔夜时段收益率的随机游走性质。 现在我来对这两种方法进行介绍并提供相应的Python代码。
\[VR^{ND} = \frac{\text{Var}\left[ R^{CC}_t \right]}{\text{Var}\left[ R^N_t \right] + \text{Var}\left[ R^D_t \right]}\]
\[VR^{DN} = \frac{\text{Var}\left[ R^{OO}_{t+1} \right]}{\text{Var}\left[ R^D_t \right] + \text{Var}\left[ R^N_{t+1} \right]}\]
Variance Ratio Test
基本原理
Variance Ratio Test由Lo and Craig MacKinlay (1988)提出，其检验原理基于时间序列在不同时间间隔上的方差是线性增长的。因此，如果一个时间序列是真正的随机游走，那么在不同时间间隔上的方差比率应该接近1。
日度频率下的VR检验统计量为：
\[VR^{CC}(q)=Var[R_t^{CC}(q)] / qVar[R_t^{CC}]\]
即间隔为\(q\)天的收益率的方差比上\(q\)倍的日度收益率的方差，其中\(R_t^{CC}(q)=lnP^C_t-lnP_{t-q}^C\)
我们现在考虑对隔夜和日度时段的收益率进行VR检验。隔夜和日内收益的拆分在此不多介绍，可以参考我们的论文。总之我们可以将t-1日收盘价到t日收盘价的收益率表示为：
\[R_t^{CC}=R_t^N+R_T^D\]
其中\(R_t^N\)表示隔夜收益，\(R_T^D\)表示日内收益。 类似地，我们可以将t日开盘价到t+1日开盘价的收益率表示为：
\[R_{t+1}^{OO}=R_t^D+R_{t+1}^N\]
那么我们就可以依照VR检验的思路，用日度收益率的方差比上日内和隔夜收益率的方差之和进行检验：
\[VR^{ND} = \frac{\text{Var}\left[ R^{CC}_t \right]}{\text{Var}\left[ R^N_t \right] + \text{Var}\left[ R^D_t \right]}\]
\[VR^{DN} = \frac{\text{Var}\left[ R^{OO}_{t+1} \right]}{\text{Var}\left[ R^D_t \right] + \text{Var}\left[ R^N_{t+1} \right]}\]
其中\(VR^{ND}\)就是对隔夜到日内的过程进行检验，\(VR^{DN}\)则是对日内到隔夜的过程进行检验。
Python代码
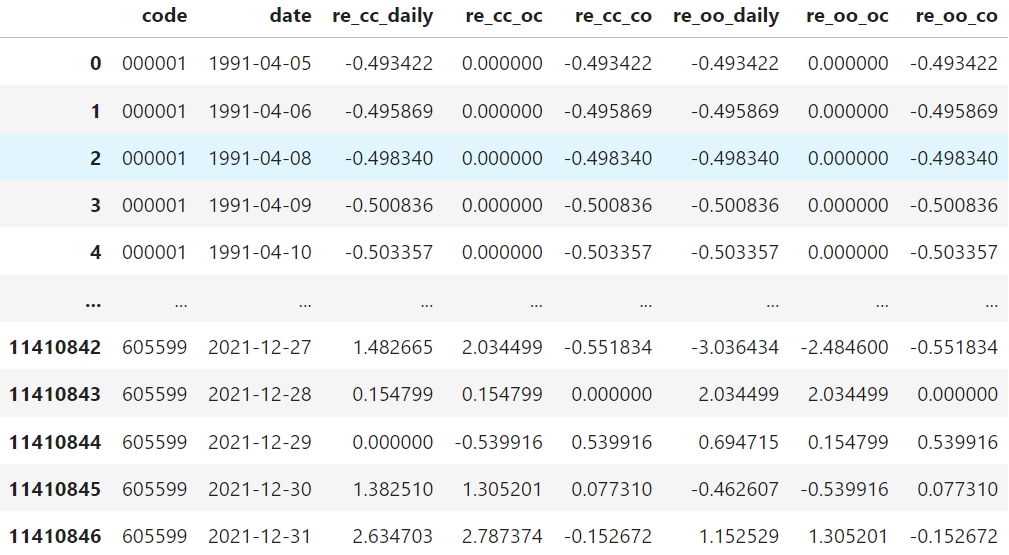
进行检验前需要准备好数据，类似下表（收益率以对数形式表示）：
变量对应
re_cc_daily, re_cc_co, re_cc_oc, re_oo_daily, re_oo_oc, re_oo_co分别对应\(R_t^{CC}, R_t^N, R_T^D, R_{t+1}^{OO}, R_t^D, R_{t+1}^N\)
我将整套VR统计量的估计方法封装到下面的函数内，该函数接收一支股票的收益率序列，返回其VR值和检验统计量
Warning
我们的论文中关心的是全部样本股票的VR，而不是单支股票的VR，因此虽然下列函数能够计算单支股票的检验统计量，但在论文的结果中并没有使用
函数参数
函数的参数code代表股票代码，log_daily_rets表示日度收益率序列，log_intraday_rets表示日内收益率序列，log_overnight_rets表示隔夜收益率序列，obs_limit表示最小观测值限制
import pandas as pd
import numpy as np
import scipy.stats as sps
def VR_estimate_stats(code,log_daily_rets, log_intraday_rets, log_overnight_rets, obs_limit):
# 添加overnight和intraday混合序列,overnight在前
mix_rets = log_intraday_rets.copy()
mix_rets.index = [i+0.5 for i in log_overnight_rets.index]
mix_rets = pd.concat([log_overnight_rets, mix_rets]).sort_index()
# 检查长度是否一致
assert len(log_daily_rets) == len(log_intraday_rets) == len(log_overnight_rets)
# T 为收益序列的长度
T = len(log_daily_rets.dropna())
# 不满足观测值要求的就返回空值
if T < obs_limit:
return pd.Series({
"code" : code,
"VR" : np.nan,
"stat_homo" : np.nan,
"stat_hetero_overnight" : np.nan,
"stat_hetero_intraday" : np.nan,
"stat_mean_daily" : np.nan,
"stat_mean_intraday" : np.nan,
"stat_mean_overnight" : np.nan,
"vr_obs" : T,
"daily_rets" : log_daily_rets.mean(),
"intraday_rets" : log_intraday_rets.mean(),
"overnight_rets" : log_overnight_rets.mean()})
# mu 为每种收益的均值
mu_daily = np.mean(log_daily_rets)
mu_intraday = np.mean(log_intraday_rets)
mu_overnight = np.mean(log_overnight_rets)
mu_mix = np.mean(mix_rets)
# demeaned_sqr 为去除均值后的序列的平方，用于计算方差等
demeaned_sqr_daily = np.square(log_daily_rets - mu_daily)
demeaned_sqr_intraday = np.square(log_intraday_rets - mu_intraday)
demeaned_sqr_overnight = np.square(log_overnight_rets - mu_overnight)
demeaned_sqr_mix = np.square(mix_rets - mu_mix)
# var_intraday 日内收益方差的估计量
var_intraday = np.sum(demeaned_sqr_intraday) / (T-1)
# var_overnight 隔夜收益方差的估计量
var_overnight = np.sum(demeaned_sqr_overnight) / (T-1)
# var_daily 全日收益率方差的估计量
# k = 2是因为daily_ret由intraday和overnight两期构成
k = 2
# m少乘一个k是因为daily_rets等于intraday_rets + overnight_rets
# 而不是某个rets的两倍
m = (T - k + 1) * (1 - k / T)
var_daily = 1/m * np.sum(demeaned_sqr_daily)
# Variance Ratio
vr = var_daily / (var_intraday + var_overnight)
# heteroscedasticity
a_arr = np.square(2 * (np.arange((k - 1), (1) - 1, step = -1, dtype = int)) / k)
# delta项的序列
# ====================overnight版本====================
b_arr_overnight = np.empty(k-1, dtype = np.float64)
for j in range(1,k):
b_arr_overnight[(j)-1] = np.sum((demeaned_sqr_mix * \
np.roll(demeaned_sqr_mix, shift = j))[(j + 1) - 1:]
)
delta_arr_overnight = b_arr_overnight / np.square(np.sum(demeaned_sqr_mix))
# ==================================================
# ====================intraday版本====================
b_arr = np.empty(k-1, dtype=np.float64)
for j in range(1, k):
b_arr[j-1] = np.sum((demeaned_sqr_mix *
np.roll(demeaned_sqr_mix, j))[j+1:])
delta_arr = b_arr / np.square(np.sum(demeaned_sqr_mix))
# ==================================================
# phi的两序列长度都应该等于k-1
assert len(b_arr_overnight) == len(delta_arr) == len(a_arr) == k-1
phi_hetero_overnight = np.sum(a_arr * delta_arr_overnight)
phi_hetero_intraday = np.sum(a_arr * delta_arr)
# homoscedasticity
phi_homo = 2 * (2*k - 1) * (k-1) / (3*k*T)
# VR test statistics
vr_stat_homo = (vr - 1) / np.sqrt(phi_homo)
vr_stat_hetero_overnight = (vr - 1) / np.sqrt(phi_hetero_overnight)
vr_stat_hetero_intraday = (vr - 1) / np.sqrt(phi_hetero_intraday)
# pvalue, two-side
vr_stat_homo_p = 2 * (1 - sps.norm.cdf(abs(vr_stat_homo)))
vr_stat_hetero_overnight_p = 2 * (1 - sps.norm.cdf(abs(vr_stat_hetero_overnight)))
vr_stat_hetero_intraday_p = 2 * (1 - sps.norm.cdf(abs(vr_stat_hetero_intraday)))
return pd.Series({
"code" : code,
"VR" : vr,
"stat_homo" : [vr_stat_homo, vr_stat_homo_p],
"stat_hetero_overnight" : [vr_stat_hetero_overnight, vr_stat_hetero_overnight_p],
"stat_hetero_intraday" : [vr_stat_hetero_intraday, vr_stat_hetero_intraday_p],
"stat_mean_daily" : sps.ttest_1samp(log_daily_rets,0),
"stat_mean_intraday" : sps.ttest_1samp(log_intraday_rets,0),
"stat_mean_overnight" : sps.ttest_1samp(log_overnight_rets,0),
"vr_obs" : T,
"daily_rets" : log_daily_rets.mean(),
"intraday_rets" : log_intraday_rets.mean(),
"overnight_rets" : log_overnight_rets.mean()})
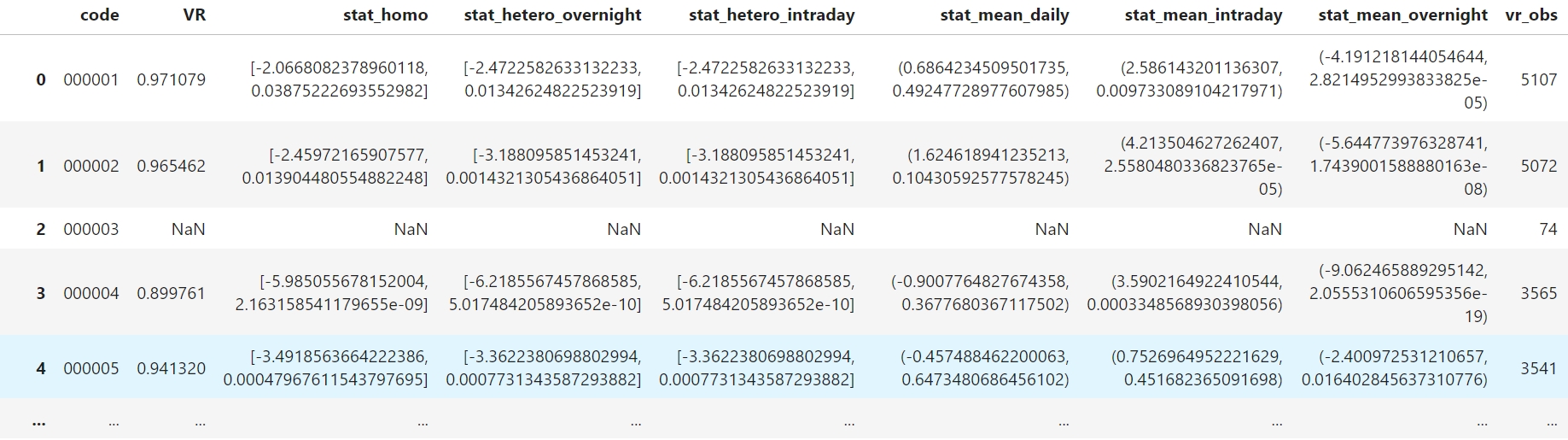
通过使用groupby方法将函数应用到每支股票的数据上，从而得到每支个股的VR检验结果，下面以检验隔夜到日内的过程为例（运行速度较慢可以考虑使用多线程对apply方法加速）：
# 以检验隔夜到日内的过程为例，先筛选出需要的数据
VR_data = (data[["code", "date", 're_cc_daily', 're_cc_oc', 're_cc_co']]
.query("date <= '2021-12-31' and date > '1999-12-31'")
.dropna()
.sort_values(["code", "date"], ascending = True))
# 使用Groupby方法间函数应用到每支股票数据上
result = VR_data.groupby("code").apply(lambda x: VR_estimate_stats(x, code = x["code"].unique()[0],
log_daily_rets = x["re_cc_daily"],
log_intraday_rets = x["re_cc_oc"],
log_overnight_rets = x["re_cc_co"],
obs_limit = 500))
运行结果如下（如果进一步对所有样本股票的VR值进行Newey-West t检验就可以得到我们论文中的结果）：
Filter Rule
基本原理
Filter Rule由Fama and Blume (1966)提出，我们对其进行了简化以适应我们的研究，其原理较为简单：
事先设定收益率阈值k，假设收益率存在动量效应，如果t-1期的收益率\(\geq\) k，那么在t期开始时多头买入；如果t-1期的收益率\(\leq\) -k，那么在t期开始时空头卖出。在t-1期结束时统一进行平仓（如果收益率存在反转效应，那么头寸方向相反）。
Tip
例如，对于隔夜到日内的过程，Variance Ratio显著小于1，可能存在反转效应。因此，如果以1%为阈值，对于个股的每个日内时段，如果之前隔夜时段收益率低于-1%，就以开盘价买入，以收盘价平仓；如果之前的隔夜时段收益率高于1%，就以开盘价卖空，以收盘价平仓 （对于日内到隔夜的过程，Variance Ratio显著大于1，可能存在动量效应，相应的Filter Rule能够根据相同的思路推导出来）。
Pyhton代码
Filter Rule的代码实现相较其原理要复杂一些，还需要考虑某些股票不具备融资融券条件的问题，因此这里不对代码进行详细说明，仅列出执行Filter Rule的主要函数，感兴趣的读者可以尝试自行理解或与我取得联系。
def determine_pos(value, thresh, below_pos, above_pos, no_pos = 0):
# 如果值大于阈值，则返回大于阈值的头寸编码
if value >= thresh:
return above_pos
# 如果值小于阈值，则返回小于阈值的头寸编码
elif value <= - thresh:
return below_pos
# 如果都不满足，则返回0
else:
return no_pos
def cal_strategy_info(longShort_pos_series, long_re_series, short_re_series, short_avl_series, year_trad_days = 242):
# 检查输入的头寸序列和收益序列的长度是否一致
if isinstance(short_avl_series, pd.Series):
assert longShort_pos_series.shape[0] == long_re_series.shape[0] == short_re_series.shape[0] == short_avl_series.shape[0], "序列长度不一致"
# 如果考虑是否允许做空，则将所有空头寸设置为空缺，然后以是否可以做空的标识序列对空缺进行填充
'''
注意：是否可以做空的标识序列需要满足0代表不允许，-1代表允许，
则填充被设置为空缺的空头寸时，允许做空则填充为-1，恢复空头寸，否则填充为0，不进行交易
'''
longShort_pos_series = longShort_pos_series.replace(-1,np.nan)
longShort_pos_series = longShort_pos_series.fillna(short_avl_series)
else:
assert longShort_pos_series.shape[0] == long_re_series.shape[0] == short_re_series.shape[0], "序列长度不一致"
# 生成只做多/做空的头寸序列，即将-1/1的头寸替换为0
long_pos_series = longShort_pos_series.replace(-1,0)
short_pos_series = longShort_pos_series.replace(1,0)
# 计算持仓天数，直接将头寸序列取绝对值并加总
N_longShort = np.abs(longShort_pos_series).sum()
N_long = np.abs(long_pos_series).sum()
N_short = np.abs(short_pos_series).sum()
# 计算仅多头、仅空头和多空策略的日平均收益。使用头寸序列与收益序列相乘再取算术平均
if N_long != 0:
avg_strategy_long_daily_re = (long_pos_series * long_re_series).sum() / N_long
else:
avg_strategy_long_daily_re = 0
if N_short != 0:
avg_strategy_short_daily_re = (short_pos_series * short_re_series).sum() / N_short
else:
avg_strategy_short_daily_re = 0
if (N_long + N_short) != 0:
avg_strategy_longShort_daily_re = (long_pos_series * long_re_series + short_pos_series * short_re_series).sum() / (N_long + N_short)
else:
avg_strategy_longShort_daily_re = 0
# 汇报的收益为日简单平均收益百分比%
return pd.Series({name_long_re : avg_strategy_long_daily_re * 100,
"long_T" : N_long,
name_short_re : avg_strategy_short_daily_re * 100,
"short_T" : N_short,
name_longShort_re : avg_strategy_longShort_daily_re * 100,
"longShort_T" : N_longShort})
def single_filter(df, _filter, pos_determine_col, return_col, below_pos, above_pos, short_avl_col = None, compelet_return = True):
df = df.copy()
# 判断交易头寸
df["pos"+f"_{_filter}"] = df[pos_determine_col].map(lambda x: determine_pos(value = x, thresh = _filter, below_pos = below_pos, above_pos = above_pos))
# 计算每支股票的多头、空头和多空策略收益和持仓天数
if short_avl_col:
trade_info = df.groupby("code").apply(lambda x: cal_strategy_info(x["pos"+f"_{_filter}"], long_re_series=x[return_col[0]], short_re_series=x[return_col[1]], short_avl_series = x[short_avl_col]))
else:
trade_info = df.groupby("code").apply(lambda x: cal_strategy_info(x["pos"+f"_{_filter}"], long_re_series=x[return_col[0]], short_re_series=x[return_col[1]], short_avl_series = None))
# 计算所有样本股票平均的持仓天数（多头持仓，空头持仓和多空持仓）
avg_long_T = trade_info["long_T"].mean()
avg_short_T = trade_info["short_T"].mean()
avg_longShort_T = trade_info["longShort_T"].mean()
# 分别对多头、空头和多空策略的收益进行t检验，并生成报告表格
report_single_filter = report_t_raw(ttest_long_short_longShort(trade_info), col_name_mapper = {"index" : "filter", "mean_report" : f"{_filter}"})
# 向报告表格中添加计算好的平均持仓天数
report_single_filter[f"{name_avgT}_{_filter}"] = report_single_filter["filter"]
report_single_filter[f"{name_avgT}_{_filter}"] = report_single_filter[f"{name_avgT}_{_filter}"].map({name_long_re : str(int(avg_long_T)),
name_short_re : str(int(avg_short_T)),
name_longShort_re : str(int(avg_longShort_T))})
report_single_filter[f"{name_avgT}_{_filter}"] = report_single_filter[f"{name_avgT}_{_filter}"].fillna("")
# 整理报告表格的格式
report_single_filter = report_single_filter.reindex(columns = ["filter", "obs", f"{name_avgT}_{_filter}", f"{_filter}"])
if compelet_return:
# 返回完整的结果，包括报告表格、每支股票的策略收益和天数以及完整的交易头寸表
return report_single_filter, trade_info, df[["code", "date", "pos"+f"_{_filter}", pos_determine_col, return_col[0]]]
else:
# 仅返回报告表格
return report_single_filter
def multi_filter(df, filter_ls, pos_determine_col, return_col, below_pos, above_pos, short_avl_col = None):
'''
return_col为一个元组或者列表，0位置为多头所用的收益，1位置为空头所用的收益
'''
df = df.copy()
# 多线程调用single_filter函数
with tqdm_joblib(tqdm(desc="Progress", total=len(filter_ls))) as progress_bar:
report_ls = Parallel(n_jobs= joblib.cpu_count())(delayed(single_filter)(df = df,
_filter = f,
pos_determine_col = pos_determine_col,
return_col = return_col,
below_pos = below_pos,
above_pos = above_pos,
compelet_return = False,
short_avl_col = short_avl_col) for f in filter_ls)
return pd.concat(report_ls, axis = 1).T.drop_duplicates().T